Drodzy uczniowie

MATEMATYKA KL.VIII

Zgodnie z wytycznymi Ministerstwa Edukacji Narodowej, przesyłam materiałydo samodzielnej pracy.

 

25 czerwca 2020r

Temat: Pola i obwody figur płaskich - trójkąty i czworokąty.

 

23 i 24 czerwca 2020r

Temat: Rozwiazywanie zadań tekstowych-powtórzenie.

 

Zadania tekstowe

Rozwiązując zadania tekstowe, czytaj zawsze bardzo uważnie, kilka razy treść zadania.

Zadania staraj się rozwiązywać według następującego schematu:

 

1. Analiza zadania: małą literą alfabetu ustalamy niewiadomą oraz układamy wyrażenia zgodnie z treścią zadania.

2. Ułożenie równania: wybieramy (z analizy zadania) takie dwa wyrażenia, które przedstawiają tę samą wielkość i łączymy je znakiem równości.

3. Rozwiązanie równania.

4. Sprawdzenie wyniku z treścią (z warunkami) zadania.

Uwaga! Ważne!

Sprawdzamy (czytając treść zadania ponownie), czy wynik spełnia warunki zadania. To nie to samo, co sprawdzenie równania, bo załóżmy, że równanie rozwiązaliśmy dobrze, ale mogliśmy popełnić błąd przy jego układaniu.

5. Podanie odpowiedzi.

Po rozwiązaniu zadania tekstowego jeszcze raz przeczytaj jego treść. Upewnij się, czy na pewno odpowiedziałeś na pytanie.

Przykładowe zadanie :

Rozwiązanie

Analiza zadania:

Ułożenie i rozwiązanie równania:

Odp.: Należy jeszcze dowieźć 65 kg soli.

Czytaj więcej na https://opracowania.pl/opracowania/matematyka/zadania-tekstowe,oid,1819#utm_source=paste&utm_medium=paste&utm_campaign=other

 

 

22 czerwca 2020r

Temat:Analiza egzaminu ósmoklasisty z matematyki.

 

Podaję link strony, na której znajdziecie rozwiazania zadań egzaminacyjnych.prosze o analizę.

https://www.rmf24.pl/raporty/raport-egzamin-osmoklasisty/2020/news-egzamin-osmoklasisty-z-matematyki-arkusze-cke-i-rozwiazania,nId,4559289

 

 

ŻYCZĘ WAM, BYŚCIE POMYŚLNIE PRZEBRNĘLI PRZEZ EGZAMIN ÓSMOKLASISTY.

SZCZEGÓLNIE PRZEZ TEN Z MATEMATYKI. POWODZENIA!

 

PROSZĘ POWTÓRZYĆ WZORY!!!

Przedstawiam rozwiązania zadań z Waszego prezentu:

 

 

 

 

 

 

Dzień dobry

Rozpakowałam dla Was prezent:

 

 Do rozwiązania zadań przydadzą się Wam zapisy:

 

 

n; n+1; n+2 - trzy kolejne liczby całkowite

 

2n; 2n+2; 2n+4 - trzy kolejne liczby parzyste

 

2n+1; 2n+3; 2n+5 - trzy kolejne liczby nieparzyste

 

10x+y - liczba dwucyfrowa, w której x oznacz cyfrę dziesiątek a y cyfrę jedności

 

130%x - liczba o 30% większa od liczby x

 

80%x - liczba o 20% mniejsza od liczby x

 

200%x - liczba o 100% większa od x , bo x to jest 100%

 

(x-y):y •100% - o ile % jest większa liczba x od y?

 

(x-y):x•100% - o ile % jest mniejsza liczba y od x?

 

 

PRZYKŁADOWE ZADANIA EGZAMINACYJNE

Zad.1

W szkole, w której uczy się 600 uczniów zorganizowano zawody z okazji dnia sportu. Uczniów biorących udział w zawodach można było podzielić na 8, 10 lub 14 równolicznych drużyn. 

 

Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D. 

 

A

B

Na stadionie mogło być minimalnie   uczniów.

 

A. 120                          B. 280

 

C

D

Na stadionie nie mogło być        uczniów. 

 

C. 360                          D. 560

 

Zad.2

Cena butów w sklepie internetowym była o 30% niższa od ceny takich butów w sklepie tradycyjnym. Buty te w sklepie internetowym były o 75 zł tańsze od takich samych butów w sklepie tradycyjnym.

 

Ile kosztowały buty w sklepie tradycyjnym? Wybierz właściwą odpowiedź spośród podanych.

 

A. 105 zł                  B. 175 zł                   C. 240 zł                  D. 250 zł                       E. 325 zł

 

Zad.3

Na wycieczkę zgłosiło się 50 dzieci, w tym 30 chłopców. W ostatnim dniu przed wyjazdem trzy dziewczynki zrezygnowały, a zamiast nich pojechało trzech chłopców.

 

Uzupełnij zdania. Wybierz poprawną odpowiedź spośród oznaczonych literami A i B oraz poprawną odpowiedź spośród oznaczonych literami C i D.

 

A

B

Liczba dziewcząt, które pojechały na wycieczkę była o mniejsza od liczby dziewcząt wcześniej zgłoszonych.

 

A. 15%                                    B. 6%

 

C

D

Na wycieczce chłopcy stanowili   wszystkich uczestników wycieczki.

 

C. 66%                                    D. 60%

 

Zad.4

W pudełku jest 7 kul białych, 5 kul czerwonych i pewna liczba kul niebieskich.

Prawdopodobieństwo wylosowania kuli niebieskiej jest równe  . 

Ile kul niebieskich jest w pudełku? Wybierz właściwą odpowiedź spośród podanych.

 

A. 1                             B. 2                             C. 3                             D. 8

 

Zad.5

W równoległoboku ABCD przekątna BD o długości a jest prostopadła do boku AD, a trójkąt ABD jest równoramienny.

 Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

 Równoległobok ABCD ma 

 

A.  obwód równy 4a.

B.   kąt ostry dwa razy mniejszy od kąta rozwartego.

C.  jeden z boków dwa razy dłuższy od drugiego.

D. pole równe a².

 

Zad.6

Najdłuższy bok trójkąta ma 12 cm, a stosunek miar kątów tego trójkąta jest równy 1 : 2 : 3.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

 

Opisany trójkąt jest prostokątny.	P	F
Najkrótszy bok trójkąta ma 4 cm.	P	F

 

 

Zad.7

Wojtek ma 15 lat, a jego mama 42. Za ile lat mama będzie dwa razy starsza  od Wojtka? Zapisz obliczenia.

 

 

 

Zad.8

Marek do zbioru truskawek przygotował jednakowe pojemniki. Pierwszego dnia zebrał z pola 28 pojemników truskawek. Drugiego dnia pracował w tym samym tempie o 3 godziny krócej niż pierwszego dnia i zebrał 16 przygotowanych pojemników truskawek. Przez ile godzin Marek zbierał truskawki pierwszego dnia? Zapisz obliczenia.

 

 

Zad.9

Dany jest równoległobok ABCD. Punkt F jest środkiem boku CD równoległoboku. Natomiast na boku AB tego równoległoboku zaznaczono punkt E tak, że odcinek EB jest trzy razy dłuższy od odcinka AE.

 

 

 

 

 

 

 

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

 

Pole trójkąta AEF stanowi 1/8  pola równoległoboku ABCD.	P	F
Pole czworokąta AEFD stanowi 1/3  pola równoległoboku ABCD.	P	F

 

 

Zad.10

Suma długości wszystkich krawędzi prostopadłościanu jest równa 60 cm. Uzasadnij, że średnia arytmetyczna długości krawędzi wychodzących z jednego wierzchołka tego prostopadłościanu jest równa 5.

 

Zad.11

Z drutu o długości 120 cm zbudowano model ostrosłupa prawidłowego trójkątnego, w którym krawędź boczna jest trzy razy dłuższa od krawędzi podstawy. Oblicz pole powierzchni całkowitej ostrosłupa o takich wymiarach. Zapisz obliczenia.

 

Zad.12

Dane są dwa równoległoboki o wymiarach podanych na rysunku.

 

 

 

 

Czy pola tych równoległoboków są równe? Wybierz odpowiedź A (Tak) albo B (Nie) i jej uzasadnienie spośród 1, 2 albo 3.

 

A.	Tak,	ponieważ	1.	wysokości tych równoległoboków poprowadzone do boków jednakowej długości są równe.
			2.	w każdym z tych równoległoboków sąsiednie boki nie są tej samej długości.
B.	Nie,
			3.	kąty ostre tych równoległoboków mają różne miary.

 

 

 

 

 Do rozwiązania zadań przydadzą się Wam zapisy:

 

 

n; n+1; n+2 - trzy kolejne liczby całkowite

 

2n; 2n+2; 2n+4 - trzy kolejne liczby parzyste

 

2n+1; 2n+3; 2n+5 - trzy kolejne liczby nieparzyste

 

10x+y - liczba dwucyfrowa, w której x oznacz cyfrę dziesiątek a y cyfrę jedności

 

130%x - liczba o 30% większa od liczby x

 

80%x - liczba o 20% mniejsza od liczby x

 

200%x - liczba o 100% większa od x , bo x to jest 100%

 

(x-y):y •100% - o ile % jest większa liczba x od y?

 

(x-y):x•100% - o ile % jest mniejsza liczba y od x?

 

 

 

15 czerwca 2020r

Temat:Rozwiązywanie przykładowych zadań egzaminacyjnych.

 

Prezent_dla_kl.8.odt

Proszę przesłać rozwiązania zadań  do 16 czerwca 2020r. do godz.16.00.

 

Witam Was.

Przedstawiam rozwiązania zadań, z którymi mieliście problemy ( ostatni test egzaminacyjny). 

Proszę o przeanalizowanie

 

 

 

 

Przypominam,że wszyscy zdajemy Egzamin Ósmoklasisty i wszystkich obowiązuje

praca. Ja też rozwiązuję te testy i wierzcie mi, że dzięki temu mózg nie ulega zanikowi.

Nauka nie boli.

Pozdrawiam Was serdecznie.

 

Witam Was.

Przedstawiam rozwiązania zadań, z którymi mieliście problemy ( ostatni test egzaminacyjny). 

Proszę o przeanalizowanie:

 

Zadanie 13

 

Zadanie 16

Zadanie 18

zadanie 21

 

10 czerwca 2020r

Temat: Rachunek prawdopodobieństwa-powtórzenie.

 

Rachunek prawdopodobieństwa zajmuje się badaniem zjawisk losowych (np. rzut monetą, rzut kostką do gry, loterie itp.) i praw rządzących tymi zjawiskami.

Doświadczenie losowe

Doświadczeniem losowym nazywamy takie doświadczenie, którego wyniku nie można przewidzieć, a przy powtarzaniu go w identycznych warunkach możemy otrzymać różne wyniki.

Każdą realizację doświadczenia losowego nazywamy wynikiem doświadczenia losowego (np. wypadło 5 oczek w rzucie kostką).

Jeśli pewne doświadczenie losowe zostało powtórzone 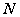 razy i dany wynik  wystąpił k razy, to liczbę  nazywamy częstością zdarzenia  w tym ciągu doświadczeń.

Należy jednak pamiętać, że w pojedynczym doświadczeniu wynik  może wystąpić lub może nie wystąpić. Powtarzając dane doświadczenie wiele razy, można zaobserwować pewną prawidłowość - częstość wyniku  stabilizuje się wraz ze wzrostem liczby doświadczeń. Jest to tzw. prawidłowość statystyczna.

 

Proszę przesłać rozwiązania zadań z grupy A, do 12 czerwca 2020r.

Racunek_prawdopodobienstwa.pdf

 

9 czerwca 2020r.

Temat: Styczna do okręgu. Pole koła.

 

Styczna do okręgu

Prosta, która ma z okręgiem tylko jeden punkt wspólny, nazywamy styczną. Styczna do okręgu, jest prostopadła do promienia, łączącego punkt styczności ze środkiem okręgu.

 

Wzór na pole koła

Pole koła liczymy wg wzoru:

P=π⋅r2

 

 

Pole koła powyżej to cały obszar zaznaczony kolorem niebieskim. 

Wzór na pole koła jest bardzo prosty, czyli używamy stałej pi (3.14) i podnosimy do kwadratu promień koła. Wynik otrzymujemy w jednostkach kwadratowych. Czyli jeżeli promień mamy wyrażony w cm (centymetrach) to wynik będzie w cm kwadratowych, jeżeli promień jest w mm (milimetrach) to wynik będzie w mm kradratowych

 

Proszę przesłać rozwiązania zadań z grupy A, do 10 czerwca 2020r.

Pole_kola.pdf

 

 

8 czerwca 2020r.

Temat:Rozwiązywanie testu egzaminacyjnego.

 

 

Rozwiązania proszę przesłać do 12 czerwca 2020r.

 

 

Jeżeli chodzi o objętość ostrosłupów, to mieliście problem z zadaniem 6. Proszę przeanalizować.

 

 

4 czerwca2020r.

Temat:Koła i okręgi - powtórzenie.

Wzór na obwód koła, to inaczej wzór na długość okręgu z wykorzystaniem promienia:

l=2⋅π⋅r

l− obwód koła lub inaczej długość okręgu
π≈3,14 − stała liczba niewymierna
r− promień okręgu

Wiemy, że dwa promienie mają długość taką samą jak średnica możemy zapisać kolejny wzór.
Wzór na obwód koła z wykorzystaniem średnicy:

l=d⋅π

d− średnica okręgu

Wzór na pole koła o danym promieniu:

P=π⋅r2

Można również spotkać trochę rzadziej wykorzystywane wzory:
Wzór na średnicę koła:

d=l/π

l− obwód koła lub inaczej długość okręgu
π≈3,14 − stała liczba niewymierna

Wzór opisujący liczbę Pi:

π=l/d

l− obwód koła lub inaczej długość okręgu
d− średnica okręgu

 

Proszę przesłać rozwiązania zadań z grupy A, do 6 czerwca 2020r.

Dlugsc_okregu.(1).pdf

 

 

PRÓBNY EGZAMIN ÓSMOKLASISTY ODBĘDZIE SIĘ 3 CZERWCA O GODZ.9.00.

Wszystkie informacje znajdziecie na stronie:

https://pistacja.tv/inspiracje/30-probne-egzaminy-z-pi-stacja

 

3 czerwca 2020r.

Temat: Objętość ostrosłupa - powtórzenie.

 

Ostrosłupem nazywamy taki wielościan, który ma jedną podstawę, a wszystkie ściany boczne zbiegają się w jednym punkcie zwanym wierzchołkiem.

Ostrosłup może mieć w podstawie dowolny wielokąt. Mówimy, że ostrosłup jest prawidłowy jeżeli ma w podstawie wielokąt foremny.

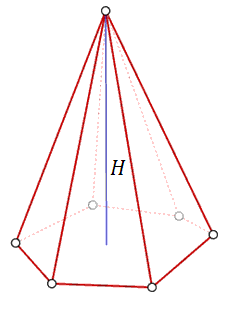Wzór na pole powierzchni ostrosłupa:

Pc=Pp+Pb

gdzie:
Pp - pole podstawy ostrosłupa
Pb - suma pól ścian bocznych ostrosłupa

Wzór na objętość ostrosłupa:

V=1/3⋅Pp⋅H

 

Proszę przesłać rozwiązania zadań z grupy A, do 4 czerwca 2020r.

V_ostroslupa.pdf

 

2 czerwca 2020r.

Temat: Pole powierzchni ostrosłupa - -powtórzenie.

 

Pole powierzchni całkowitej to suma pól powierzchni wszystkich ścian danej bryły. W przypadku ostrosłupów będzie do suma pola podstawy oraz wszystkich ścian bocznych.

Wzór na pole powierzchni całkowitej zależy w dużej mierze od tego jaki to jest ostrosłup (zwłaszcza od tego co znajduje się w podstawie), ale w dużym uproszczeniu możemy zapisać, że:

Pc=Pp+Pb

 

gdzie:
Pc – pole powierzchni całkowitej
Pp – pole podstawy
Pb – pole powierzchni bocznej (czyli suma wszystkich pól ścian bocznych)

Proszę przesłać rozwiązania zadań z grupy A, do 3 czerwca 2020r.

Pole_ostr..pdf

 

Z OKAZJI DNIA DZIECKA, ŻYCZĘ WAM SAMYCH DOBRYCH DNI.

(szczególnie podczas egzaminu:).

 

1 czerwca 2020r

Temat:Pole powierzchni i objętość graniastosłupa.

 

Objętość dowolnego graniastosłupa jest opisana wzorem:

 

Pole powierzchni całkowitej dowolnego graniastosłupa P_c dane jest wzorem:

 

Proszę przesłać rozwiązania zadań z grupy A, do 2 czerwca 2020r.

Graniast..pdf

 

Ponadto, z okazji Dnia Dziecka, mam dla Was prezent w postaci testu egzaminacyjnego.

Rozwiązania proszę przesłać do 6 czerwca 2020r.

 

 

 

 

Witam Was serdecznie.

Przedstawiam rozwiązania zadań, z którymi mieliście problemy ( ostatni test egzaminacyjny). 

Proszę o przeanalizowanie:

28 maja 2020r.

Temat: Figury geometryczne-powtórzenie.

Proszę przesłać rozwiązania zadań z grupy A, do 30 maja 2020r.

Fig.na_pl..pdf

 

27 maja 2020r.

Temat: Zastosowanie twierdzenia Pitagorasa do rozwiązywania zadań.

 

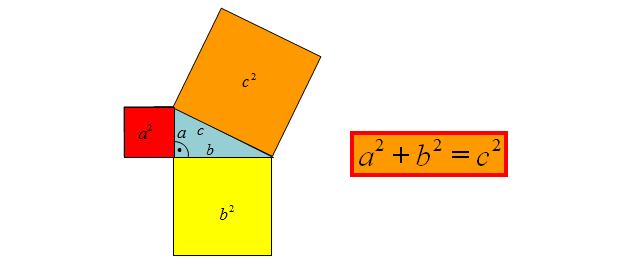
Twierdzenie Pitagorasa:

„Jeżeli trójkąt jest prostokątny, to suma kwadratów dwóch przyprostokątnych jest równa kwadratowi przeciwprostokątnej”.

Twierdzenie Pitagorasa, rysunek i wzór:

Proszę przesłać rozwiązania zadań z grupy A, do 28 maja 2020r.

Zast_tw.Pitagorasa.pdf

 

 

26 maja 2020r.

Temat:Trójkąty i czworokaty - powtórzenie.

 

Wszystkie własności trókątów i czworokątów znajdziecie w podręczniku na stronie 73 i 74,

co pomoże Wam rozwiązać zadania z pracy domowej.

 

Proszę przesłać rozwiązania zadań z grupy A, do 27 maja 2020r.

Trojkaty_i_czworokaty.pdf

 

25 maja 2020r.

Temat:Wyrażenia algebraiczne i równania-powtórzenie.

 

Proszę przesłać rozwiązania zadań z grupy A,  do 26 maja 2020r.

Wyrazenia_i_rownania.pdf

 

21 maja 2020r.

Temat: Liczby i działania, równania - powtórzenia wiadomości.

 

Pragniemy dobrze zdać egzamin, więc mam dla Was propozycję:

Proszę postępować według poniższej instrukcji i wykonać zadania z zestawu nr 1 oraz

 z zestawu nr 2  do 22 maja 2020r. Loginy i hasła prześlę Wam przez messengera lub pocztę.

Podczas logowania ,proszę podać imię i nazwisko, a nie numer z dziennika.

powtorkomat.gwo.pl - zaloguj się - moje dostępy - PowtórkoMat8 - start - Testy sprawdzające - Zestaw nr...

W razie problemów proszę się do mnie odzywać.

 

 

 

Witam Was :)

Przedstawiam rozwiązania zadań, z którymi mieliście problemy. Proszę o przeanalizowanie:

 

 

19 i 20 maja 2020r.

Temat: Rozwiązywanie testu egzaminacyjnego.

UWAGA!!!

DO WSZYSTKICH ZADAŃ ROBICIE OBLICZENIA (chyba, że odpowiedź jest oczywista). BEZ OBLICZEŃ Op.

 

 

 

 

Rozwiązania proszę przesłać do 25 maja 2020r.

Proszę podejść poważnie do pracy, bo niedługo piszemy egzamin!!!

 

18 maja 2020r.

Temat: :Rozwiązywanie zadań tekstowych za pomocą równań I-go stopnia z jedną niewiadomą.

ZADANIA TEKSTOWE

Zadanie 1. (2pkt) Paweł kupił australijski znaczek i 3 znaczki krajowe. Każdy znaczek krajowy kosztował tyle samo. Za wszystkie znaczki zapłacił 16zł. Ile kosztował znaczek australijski, jeżeli był pięciokrotnie droższy niż znaczek krajowy?

 

Zadanie 2. (3pkt) Marcin przebywa autobusem 3/4 drogi do jeziora, a pozostałą część piechotą. Oblicz odległość między domem Marcina, a jeziorem, jeżeli trasa, którą przebywa pieszo, jest o 8km krótsza niż trasa, którą przebywa autobusem.

 

Zadanie 3. (2pkt) Podczas trzydniowej pieszej wycieczki uczniowie przeszli 39km. Drugiego dnia pokonali dwa razy dłuższą trasę niż pierwszego dnia, a trzeciego o 5km mniej niż pierwszego. Ile km przebyli pierwszego dnia?

 

Zadanie 4. (4pkt) Na rzece zbudowano most, który zachodzi na jej brzegi: 150 metrów mostu zachodzi na jeden brzeg, a 1/3 długości mostu na drugi. Oblicz szerokość rzeki, jeżeli stanowi ona 1/6 długości mostu.

Zadanie 5. (5pkt) Poniższej przedstawiono ceny paliw:

-cena benzyny: 3,80 zł/l

-cena gazu: 1,60 zł/l

Montaż instalacji gazowej w samochodzie 2208zł. Samochód spala średnio 7 litrów benzyny lub 8 litrów gazu na każde 100km drogi. Oblicz, po ilu miesiącach zwrócą się koszty instalacji, jeśli w ciągu miesiąca samochód przejeżdża średnio 2000km.

 

Zadanie 6. (3pkt) Uczniowie klas trzecich pewnego gimnazjum pojechali na wycieczkę pociągiem. W każdym zajętym przez nich przedziale było ośmioro uczniów. Jeśli w każdym przedziale byłoby sześcioro uczniów, to zajęliby oni o 3 przedziały więcej. Ilu uczniów pojechało na tę wycieczkę?

 

Zadanie 7. (1pkt) Trzy lata temu posadzono przed domem krzew. Co roku podwajał on swoją wysokość i teraz ma 144cm. Jeśli przez x oznaczymy wysokość krzewu w dniu posadzenia, to informacjom z zadania odpowiada równanie:

A) x=144

B) 4x=144

C) 6x=144

D) 8x=144

 Przypominam, że do zadań z treścią, należy napisać odpowiedź.

Rozwiązania zadań proszę przesłać do 19 maja 2020r.

 

14 maja 2020r.

Temat:Rozwiazywanie zadań tekstowych za pomocą równań I-go stopnia z jedną niewiadomą.

Rozwiązywanie zadań tekstowych za pomocą równań

Etapy rozwiązywania zadań tekstowych

Niektóre zadania tekstowe można rozwiązać zarówno arytmetycznie, wykonując różne działania, jak i za pomocą równań. Są także takie zadania, które najprościej rozwiązuje się układając i rozwiązując odpowiednie równanie. Po przeczytaniu zadania nie zawsze od razu wiemy, jak je rozwiązać, dlatego ważny jest zapis danych i kolejnych etapów rozwiązania.
Jeżeli zadanie tekstowe rozwiązujemy za pomocą równania, to trzeba zwrócić szczególną uwagę na poprawny zapis rozwiązania. Najlepiej jest wtedy stosować się do pewnego schematu i po uważnym przeczytaniu treści pokonywać kolejne etapy rozwiązywania zadania:

1. Ustal niewiadomą w zadaniu, oznacz ją dowolną literą, np. xx.

2. Wykorzystaj dane z zadania i niewiadomą, zapisuj i opisuj różne wyrażenia algebraiczne aż pojawią się dwa oznaczające to samo.

3. Ułóż równanie opisujące sytuację z zadania.

4. Rozwiąż równanie.

5. Sprawdź z warunkami zadania, czy rozwiązanie jest poprawne.

6. Sformułuj odpowiedź do zadania.

 

Przykład:

Rozwiążmy za pomocą równania następujące zadanie tekstowe:
Lucynka kupiła 5 jednakowych zeszytów i piórnik za 12 zł. Za te zakupy zapłaciła 18 zł. Ile kosztował jeden zeszyt?
Poniżej jest rozwiązanie tego zadania z ponumerowanymi etapami.

Tabela. Dane

1.	x – cena zeszytu
2.	5x – koszt wszystkich zeszytów 5 x + 12 – zapłacona kwota 18
3.	5x + 12 = 18
4.	5x = 18 – 12 5x = 6 x = 6 : 5 x = 1,2
5.	Odpowiedź: Jeden zeszyt kosztował 1,2 zł

 

Zadania:13,14,15 i 16 ze str.54

 

 

 

12 i 13 maja 2020r.

Temat: Rozwiązywanie testu egzaminacyjnego.

zeszyt-cwiczen-matematyka-z-kluczem-klasa-8-czesc-1_(2)(5).pdf

Rozwiązania (strona od 97 do 101), proszę przesłać do 18 maja 2020r.

 

11 maja 2020r.

Temat: Rozwiązywanie równań I-go stopnia z jedna niewiadomą

Rozwiązywanie równań z jedną niewiadomą

Równanie z jedną niewiadomą znaczy, że w równaniu jest tylko jedna niewiadoma x i to w pierwszej potędze. Rozwiązaniem takiego równania jest znalezienie takiej liczby, która spełni to równanie, czyli wyznaczenie  x.

Zadania:4/52 oraz 6,7/53

 

7 maja 2020r.

Temat:Równania I-go stopnia z jedną niewiadomą-powtórzenie..

 

Rozwiązania proszę przesłać do 10 maja 2020r.

 

6 maja2020r.

Temat: Obliczanie wartości wyrażeń algebraicznych.

 

Obliczanie wartości liczbowej wyrażenia algebraicznego

Aby obliczyć wartość liczbową wyrażenia algebraicznego, należy podstawić w miejsce literek liczby.

Przykład 1.

Oblicz wartość liczbową wyrażenia 3x2−2x+1 dla x=5.

Rozwiązanie:

Do wyrażenia algebraicznego

3x2−2x+1

podstawiamy w miejsce x-a liczbę 5:

3⋅52−2⋅5+1=3⋅25−10+1=66

Zatem dla x=5 wyrażenie 3x2−2x+1 przyjmuje wartość 66.

Przykład 2.

Oblicz wartość liczbową wyrażenia −x3−(x+1)2 dla x=4.

Rozwiązanie:

Do wyrażenia algebraicznego

−x3−(x+1)2

podstawiamy w miejsce x-a liczbę 4:

−43−(4+1)2=−64−25=−89

Zatem dla x=4 wyrażenie −x3−(x+1)2 przyjmuje wartość −89.

Zadania:9 i 13 str.48

 

5 maja 2020r.

Temat:Przekształcenia algebraiczne-zapisywanie wyrażeń algebraicznych.

Proszę obejrzeć filmik i wszystko sobie przypomnicie:

https://www.youtube.com/watch?v=rHaXQROxO6o

Zadania:1 i 2 str. 47

 

4 maja 2020r.

Temat;Liczby i działania - powtórzenie.

questions.pdf

Proszę rozwiązać zadania z grupy A i przesłać do 4 maja 2020r.

 

Przedstawiam Wam rozwiązania Powtórki z CKE - 1 dzien. Kto z Was miał problem z rozwiązaniem zadań, proszę przeanalizować           .powtorki-z-cke-dzien-1.pdf

 

 

 

30 kwietnia 2020r.

Temat: Rozwiązywanie testu egzaminacyjnego.

 

 

zeszyt-cwiczen-matematyka-z-kluczem-klasa-8-czesc-1_(2)(4).pdf

Rozwiązania ( strona 92,93,94,95,96)  proszę przesłać do 6 maja 2020r.

 

 

29 kwietnia 2020r.

Temat: Liczby i działania. Działania na potęgach i pierwiastkach.

 

Działania na potęgach:

 

Działania na pierwiastkach:

Praca domowa strona 14 i 15 z poniższej powtórki. Rozwiązania proszę przesłać

do 30 kwietnia 2020 r.

powtorki-z-cke-dzien-1.pdf

 

28 kwietnia 2020r.

Temat: Działania na liczbach. Zamiana jednostek.

 

Długość
Zmiana jednostek długości

W układzie  podstawową jednostką długości jest metr 

Pole powierzchni
Zamiana jednostek pola

Objętość
Zamiana jednostek objętości

Pojemność
Zamiana jednostek pojemności

Masa
Zamiana jednostek masy

W układzie  podstawową jednostką masy jest kilogram 

Czas
Zamiana jednostek czasu

W układzie  podstawową jednostką czasu jest sekunda 

Zadania:2,3,4 str 29

 

27 kwietnia 2020r.

Temat: Zapisywanie liczb w notacji wykładniczej.

 

Notacja wykładnicza

Co to jest notacja wykładnicza?

Notacja wykładnicza pomaga w zapisywaniu bardzo dużych i małych liczb, których zapis byłby znacząco wydłużony i sprawiałby kłopot w ich odczytaniu.

Wyobraź sobie liczbę: 3 000 000 000 000. Składa się ona z cyfry 3 i z 12 zer.

Zatem 3 000 000 000 000 można zapisać krócej, jako 3 · 10¹²

Spójrz na liczbę: 0,000 000 000 000 000 000 005. Ma ona 27 miejsc po przecinku. Można ją zapisać znacznie krócej, jako 5 · 10^-27. Zobacz, jak wygląda potęga o wykładniku całkowitym ujemnym?

Postać notacji wykładniczej:    a · 10^x

a – jest liczbą (mantysą) z przedziału [1,10)

x – jest całkowitym wykładnikiem.

Zapisując liczbę w notacji wykładniczej przesuwasz przecinek w liczbie tak, aby otrzymać najpierw liczbę (mantysę) z przedziału [1,10), a następnie mnożysz ją przez 10 do pewnej potęgi x.

W dużych liczbach mantysa jest mniejsza od danej liczby o y miejsc po przecinku. Notacja wykładnicza jest wówczas zapisywana jako iloczyn mantysy z przedziału [1,10) razy 10 do potęgi y.

W bardzo małych liczbach mantysa jest większa od danej liczby o y miejsc po przecinku. Notację wykładniczą tworzymy, mnożąc mantysę przez 10 do potęgi -y.

W zrozumieniu tematu może Wam pomóc również film:

https://www.youtube.com/watch?v=Vis7HKIt60U

Zadania:10,11 i 12 ze str. 25

 

23 kwietnia 2020r.

Temat: Porównywanie liczb. Liczby przeciwne i odwrotne.

 

LICZBY PRZECIWNE, LICZNY ODWROTNE

W zbiorze liczb rzeczywistych definiujemy liczby przeciwne i liczby odwrotne.

Liczba przeciwna do liczby a, to liczna b taka, że a+b=0.

Przekształcając powyższe równanie otrzymujemy, że liczbą przeciwną do liczby a jest liczba −a. Jedna liczba jest przeciwna do drugiej, jeśli ma taką samą wartość bezwzględną, ale przeciwny znak. Na osi liczbowej dwie liczby przeciwne znajdują się w tej samej odległości od zera, ale po przeciwnych stronach punktu zerowego.

Przykłady
Liczbą przeciwną do liczby 5 jest liczba −5.
Liczbą przeciwną do liczby −10 jest liczba 10.
Liczbą przeciwną do liczby 0.7 jest liczba −0.7.
Liczbą przeciwną do liczby 34 jest liczba −34.
Liczbą przeciwną do liczby −12 jest liczba 12.
Liczbą przeciwną do liczby 2√ jest liczba −2√.
Liczbą przeciwną do liczby 3+3√ jest liczba −3−3√.
W szczególności liczbą przeciwną do 0 jest liczba 0.

 

Liczba odwrotna do liczby a, to liczna b taka, że a⋅b=1.

Przekształcając powyższe równanie otrzymujemy, że liczbą odwrotną do liczby a jest liczba 1a. Ułamek 1a możemy zapisać w postaci a−1, a więc liczbą odwrotną do liczby a to liczba a−1, z zastrzeżeniem, że a≠0. Nie istnieje liczba odwrotna do liczby 0. W szczególności liczbą odwrotną do liczby wymiernej qp jest liczba qp, ponieważ ich iloczyn równy jest zawsze 1.

Przykłady
Liczbą odwrotną do liczby 5 jest liczba 15, bo 15⋅5=1.
Liczbą odwrotną do liczby −10 jest liczba −110, bo −110⋅(−10)=1.
Liczbą odwrotną do liczby 0.7 jest liczba 107, bo 107⋅0.7=1.
Liczbą odwrotną do liczby 34 jest liczba 43, bo 43⋅34=1.
Liczbą odwrotną do liczby −12 jest liczba −2, bo −2⋅(−12)=1.
Liczbą odwrotną do liczby 2√ jest liczba 12√, bo 12√⋅2√=1.
Liczbą odwrotną do liczby 3+3√ jest liczba 13+3√, bo 13+3√⋅(3+3√)=1.

Zadania 1,2 str.23 i 8 str 25

 

 

22 kwietnia 2020r.

Temat:Własności liczb naturalnych - cechy podzielności liczb.

 

PODZIELNOŚĆ PRZEZ 2

Liczba będzie podzielna przez 2, jeżeli na końcu tej liczby będzie stała któraś z następujących cyfr:0, 2, 4, 6, 8. Nie jest ważne jakie cyfry są wcześniej, interesuje nas tylko ostatnia cyfra.

Przykłady liczb:

20, 552, 7894, 95736, 678368

PODZIELNOŚĆ PRZEZ 3

Liczba będzie podzielna przez 3, jeżeli suma wszystkich cyfr tej liczby jest podzielna przez 3.

Przykłady liczb:

1110, ponieważ 1+1+1+0=3, a wiemy, że każda liczba dzieli się przez samą siebie, więc 3 również dzieli się przez 3

2403, ponieważ 2+4+0+3=9, a wiemy, że 9 dzieli się przez 3

 

PODZIELNOŚĆ PRZEZ 4

 

Liczba będzie podzielna przez 4, jeżeli liczba złożona z dwóch ostatnich cyfr jest podzielna przez 4. Tutaj również nie interesują na cyfry wcześniejsze, sprawdzamy tylko dwie ostatnie.

Przykłady liczb:

345678912, ponieważ 12 dzieli się przez 4

45604, w takim przypadku rozpatrujemy tylko ostatnią cyfrę, czyli 4 dzieli się przez 4

 

PODZIELNOŚĆ PRZEZ 5

 

Liczba będzie podzielna przez 5, jeżeli na końcu tej liczby będzie stała cyfra 0 lub 5.

Przykłady liczb:

45, 988540, 567324565

PODZIELNOŚĆ PRZEZ 9

Liczba będzie podzielna przez 9, jeżeli suma wszystkich cyfr tej liczby jest podzielna przez 9. Zauważ, że ta zasada jest podobna do zasady podzielności przez 3, z tym, że suma musi być podzielna przez 9.

Przykłady liczb:

303021, ponieważ 3+0+3+0+2+1=9, a wiemy, że liczba 9 jest podzielna przez samą siebie, czyli przez 9

5416317, ponieważ 5+4+1+6+3+1+7=27, a wiemy, że 27 dzieli się przez 9

 Zadania: 6,7 i 8 ze str.18

 

 

21 kwietnia 2020r.

Temat Zapisywanie i odczytywanie liczb w systemie rzymskim.

Rzymski system zapisywania liczb

Pierwotny rzymski system zapisywania liczb był prosty, ale dość niewygodny. Rzymianie zapisywali liczby za pomocą tylko pionowych kresek, na kształt systemu karbowego. Wprowadzono więc dla oznaczenia ważnych liczb dodatkowe znaki.

Rzymski sposób zapisywania liczb jest sposobem addytywnym, czyli wartość danej liczby określa się na podstawie sumy wartości jej znaków cyfrowych. Wyjątki od tej zasady to liczby: 4, 9, 40, 90, 400 i 900, do opisu których używa się odejmowania. Podczas zapisywania liczb w systemie rzymskim należy dążyć zawsze do tego, aby używać jak najmniejszej liczby znaków, pamiętając przy tym o zasadach:

4. Znakami poprzedzającymi znak oznaczający większą liczbę mogą być tylko znaki: I, X, C.
3. Nie może być dwóch znaków oznaczających liczby mniejsze bezpośrednio przed znakiem oznaczającym liczbę większą.
2. Obok siebie nie mogą stać dwa znaki: V, L, D.
1. Obok siebie mogą stać co najwyżej trzy znaki spośród: I, X, C lub M.

Za pomocą dostępnych znaków można zapisać liczby od 1 do 3999, ponieważ nie istnieją znaki dla liczb większych od 1000. 

 Zadania: 1,2, 3 i 4 ze str.12

 

 

20 kwietnia 2020r.

Temat: Rozwiązywanie testu egzaminacyjnego.

 

16 kwietnia 2020r.

Temat: Rozwiązywanie testu egzaminacyjnego.

teraz-egzamin-osmoklasisty-arkusz-3-do-powtorek.pdf

PROSZĘ ROZWIĄZANIA PRZESŁAĆ DO 23 KWIETNIA 2020r.

 

15 kwietnia 2020r.

Temat:Ile jest możliwości? - powtórzenie wiadomości.

Zadania:5,6,7 i 8 ze str.270. Rozwiązania proszę przesłać do 16 kwietnia2020r.

 

7 i 8 kwietnia 2020r.

Temat: Powtórzenie wiadomości z rachunku prawdopodobieństwa.

Zadania:1,2,3, i 4 ze str.270.

PROSZĘ PRZYSŁAĆ TEST "PRZED KLASÓWKĄ"  DO SPRAWDZENIA DO 8 KWIETNIA 2020r.

 

6 kwietnia 2020r.

Temat:Rachunek prawdopodobieństwa-powtórzenie.

Zadania: Test "Przed klasówką" str. 269.

 

Witam Was ponownie. Mam dla Was kolejny test egzaminacyjny. Proszę o przesłanie rozwiązań do 4 kwietnia 2020r.

teraz-egzamin-osmoklasisty-arkusz-2-do-powtorek.pdf

 

2 kwietnia 2020r.

Temat: Obliczanie prawdopodobieństw.

Zadania: 1,2 str.266 oraz 3,4 str. 267.

 

1 kwietnia 2020r.

Temat: Rachunek prawdopodobieństwa-ile jest możliwości?.

Zadania: 11,12/263 oraz 13 i 14/264.

 

31 marca 2020r.

Temat: Egzamin próbny z matematyki.

 

 

30 marca 2020r.

Temat: Ile jest możliwości?

Zadania: 7,8,9,10 str.263.

 

25,26 marca 2020r.

Temat:Ile jest możliwości?

Zadania: 1,2,3,4,5,6 ze str. 262.

 

24 marca 2020 r.

  Temat: Rozwiązywanie testu egzaminacyjnego.

Proszę o przesłanie rozwiązań testu egzaminacyjnego, do 28 marca 2020r, przez Messengera.

teraz-egzamin-osmoklasisty-arkusz-1-do-powtorek(7).pdf

 

17 ,18 ,19 i 23  marca 2020 r.

Temat: Symetrie-powtórzenie wiadomości.

Zadania: 2,4,5,6,11str 230 oraz 13,15,16 str231

 Przed klasówką str 228 i 229 w podręczniku.

Zadania: 18,20,21,23 str 231

 

16 marca 2020 r.

Temat: Środek symetrii figury.

Zadania: 1,2,3 str.225 oraz 6,7,8,9,19 str.226

 

12 marca 2020 r.

Temat:Symetria względem punktu.

Zadania: 3,4 str.222 oraz 7,8,9 str.223

Srawdź czy umiesz str. 224

 

16 marca 2020 r.

Temat: Środek symetrii figury.

Zadania: 1,2,3 str.225 oraz 6,7,8,9,19 str.226

 

 

 

 

Ponadto, przypominam o zbliżającym się terminie egzaminu ósmoklasisty i dlatego proponuję wejść na stronę:

https://szaloneliczby.pl/egzamin-osmoklasisty/

 

„Nauka to pokarm dla rozumu.”

– Lew Tołstoj

Do miłego zobaczenia.